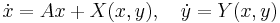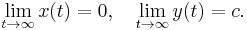Lyapunov–Malkin theorem
The Lyapunov–Malkin theorem (named for Aleksandr Lyapunov and Ioel Gilevich Malkin) is a mathematical theorem detailing nonlinear stability of systems.[1]
Theorem
In the system of differential equations,
where, 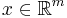 ,
, 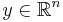 ,
,  in an m × m matrix, and X(x, y), Y(x, y) represent higher order nonlinear terms. If all eigenvalues of the matrix
in an m × m matrix, and X(x, y), Y(x, y) represent higher order nonlinear terms. If all eigenvalues of the matrix  have negative real parts, and X(x, y), Y(x, y) vanish when x = 0, then the solution x = 0, y = 0 of this system is stabile with respect to (x, y) and asymptotically stable in respect to x. If a solution (x(t), y(t)) is close enough to the solution x = 0, y = 0, then
have negative real parts, and X(x, y), Y(x, y) vanish when x = 0, then the solution x = 0, y = 0 of this system is stabile with respect to (x, y) and asymptotically stable in respect to x. If a solution (x(t), y(t)) is close enough to the solution x = 0, y = 0, then